In this post we’ll characterize all of the irreducible representations of 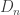 over an algebraically closed field
over an algebraically closed field  . We will suppose
. We will suppose  so that Maschke’s theorem holds and
so that Maschke’s theorem holds and  has finite representation type.
has finite representation type.
First, let’s recall the following corollary of the Artin-Wedderburn theorem:
Corollary: Let  be a finite group such that the group algebra
be a finite group such that the group algebra  is semisimple. Let
is semisimple. Let  be a complete system of representatives for the isomorphism classes of simple
be a complete system of representatives for the isomorphism classes of simple  -modules and let
-modules and let  and
and  , so that there’s an isomorphism of algebras
, so that there’s an isomorphism of algebras  . Then:
. Then:
(i)  (the so-called sum-of-squares formula).
(the so-called sum-of-squares formula).
(ii) If  , then
, then  .
.
(iii) If  is algebraically closed and
is algebraically closed and  then
then  .
.
(iv) If  is algebraically closed, the number of simple modules
is algebraically closed, the number of simple modules 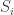 of
of  -dimension 1 is exactly the same as
-dimension 1 is exactly the same as  .
.
(v)  (where
(where  stands for the set of conjugacy classes of
stands for the set of conjugacy classes of  ) and the equality holds if
) and the equality holds if  is algebraically closed.
is algebraically closed.
Let’s begin with our characterization. Let  be an irreducible
be an irreducible  -dimensional representation of
-dimensional representation of 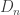 , and recall that
, and recall that  is a presentation for
is a presentation for 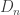 . The equation
. The equation  implies that the matrix representing
implies that the matrix representing  (which we’ll simply call
(which we’ll simply call  for the remainder of this post) is diagonalizable, since its minimal polynomial divides
for the remainder of this post) is diagonalizable, since its minimal polynomial divides 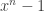 , which has simple roots because of our hypothesis on the characteristic of the field. Moreover, every eigenvalue of
, which has simple roots because of our hypothesis on the characteristic of the field. Moreover, every eigenvalue of  is an
is an  -th root of unity.
-th root of unity.
Suppose that  ; since
; since  has an eigenvector
has an eigenvector  , then
, then  is a non-trivial subrepresentation of
is a non-trivial subrepresentation of  and so must be
and so must be  by irreducibility. In this case,
by irreducibility. In this case,  is a
is a  matrix such that
matrix such that  , so
, so  . Both possibilities can occur, and in fact correspond to the trivial and sign representations, respectively.
. Both possibilities can occur, and in fact correspond to the trivial and sign representations, respectively.
Now, if  , take
, take  an eigenvector of
an eigenvector of  with eigenvalue
with eigenvalue  . Then
. Then  ; and so
; and so  . One now can easily check that
. One now can easily check that  is a subrepresentation, and we see that
is a subrepresentation, and we see that  has dimension at most
has dimension at most  . Therefore, in this case, the representation is given by
. Therefore, in this case, the representation is given by

Recall that  was an
was an  -th root of unity. If
-th root of unity. If  is even, then
is even, then 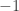 is an
is an  -th root of unity, and so picking
-th root of unity, and so picking  makes
makes  a scalar matrix. Therefore any eigenvalue of
a scalar matrix. Therefore any eigenvalue of  gives rise to a
gives rise to a  -dimensional subrepresentation. This makes sense, since
-dimensional subrepresentation. This makes sense, since  is
is 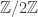 or
or  , and so we’ll have a different number of irreducible representations of dimension
, and so we’ll have a different number of irreducible representations of dimension  depending on the parity of
depending on the parity of  .
.
In any other case, that is,  , this representation is clearly irreducible since
, this representation is clearly irreducible since  and
and  share no eigenvalues.
share no eigenvalues.
It’s easy to see that if 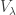 denotes the irreducible representation we just described, then
denotes the irreducible representation we just described, then  . Let’s prove that if
. Let’s prove that if  and
and  , then
, then  . By (i)
. By (i)  ; and since
; and since  (a finite dimensional
(a finite dimensional  -algebra which is a domain must be a field; and therefore
-algebra which is a domain must be a field; and therefore 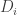 is a finite extension of
is a finite extension of  , which is algebraically closed) we have that
, which is algebraically closed) we have that  in the odd case and
in the odd case and  in the even case. An easy counting argument then shows that our
in the even case. An easy counting argument then shows that our 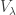 representations are pairwise non-isomorphic, as we wanted.
representations are pairwise non-isomorphic, as we wanted.
This completely classifies the representations of 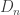 , as every representation is a direct sum of the irreducible representations we just classified.
, as every representation is a direct sum of the irreducible representations we just classified.
Moreover, we can give explicit submodules of  isomorphic to each simple module. Given any character
isomorphic to each simple module. Given any character  , the submodule
, the submodule  is isomorphic to the simple module of dimension
is isomorphic to the simple module of dimension  associated with the character
associated with the character  . This construction works in general for any representation induced by a character. Now, for the
. This construction works in general for any representation induced by a character. Now, for the  -dimensional case, we have that the submodule
-dimensional case, we have that the submodule  is isomorphic to the simple submodule
is isomorphic to the simple submodule 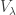 .
.
be a singular rational projective cubic. It follows from Bézout’s theorem (applied over
) that there can only be one singularity; if not, the line joining two singularities would intersect
with total multiplicity at least
, but a cubic and a line intersect with multiplicity at most
. Moreover, another application of Bézout’s theorem proves that the singularity must be a double point; if it were higher, once again we’d arrive at a contradiction after joining the singularity and another point of the curve with a line.
. We know that
‘s coordinates are algebraic over
, so we can pick a finite Galois extension
containing all of them. Now, we consider the action of the Galois group
over
. Since the Galois group acts on curves, it must preserve its singularities (since a singularity is a common zero of both
and its derivatives). Therefore, it must fix
, and so we conclude that
is a rational point.
with rational slope must intersect the cubic exactly one more time (once again by Bézout). Thus, we completely parameterize the cubic’s rational points in terms of its singularity.



