(This post is a solution to problem 1.26 from Etingof, Goldberg and Hensel’s text on representation theory).
In this post we will study the representation theory of the Weyl algebra  , where
, where  is algebraically closed.
is algebraically closed.
If the characteristic of the field  is zero, then there are no non-trivial finite dimensional representations of
is zero, then there are no non-trivial finite dimensional representations of  , since in such a representation
, since in such a representation 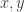 must act as matrices and the identity
must act as matrices and the identity ![[x,y]=1](https://s0.wp.com/latex.php?latex=%5Bx%2Cy%5D%3D1&bg=ffffff&fg=333333&s=0&c=20201002) cannot hold since the commutator of two matrices has null trace, while the identity does not.
cannot hold since the commutator of two matrices has null trace, while the identity does not.
It is easy to prove by induction that  . Suppose then that
. Suppose then that  is a bilateral ideal of
is a bilateral ideal of  containing a non-zero element
containing a non-zero element 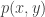 , in which we will suppose that both variables appear with non-zero coefficients. The previous identity shows that
, in which we will suppose that both variables appear with non-zero coefficients. The previous identity shows that  (in fact,
(in fact, 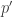 is the derivative of
is the derivative of  with respect to
with respect to  evaluated at
evaluated at 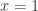 ), so we may always find a polynomial
), so we may always find a polynomial  depending on only one variable in any ideal. This shows that the only non-zero ideal is in fact the whole algebra, since if
depending on only one variable in any ideal. This shows that the only non-zero ideal is in fact the whole algebra, since if 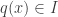 then so does
then so does  which is a unit in the algebra. This in turn provides another proof of the fact that there are no non-trivial finite dimensional representations, since such a representation is given by a map of algebras
which is a unit in the algebra. This in turn provides another proof of the fact that there are no non-trivial finite dimensional representations, since such a representation is given by a map of algebras  , and since the latter is finite-dimensional we necessarily have non-trivial kernel. Since the kernel is an ideal in
, and since the latter is finite-dimensional we necessarily have non-trivial kernel. Since the kernel is an ideal in  , it follows that
, it follows that  , and in particular its unit, must act as
, and in particular its unit, must act as  , which proves that
, which proves that  .
.
Suppose now that our base field has positive characteristic  . The commutation relation easily shows that
. The commutation relation easily shows that  are central, since
are central, since  . We claim that the center is exactly the ideal
. We claim that the center is exactly the ideal  . If not, suppose
. If not, suppose  is a polynomial not contained in this ideal. Without loss of generality we will assume that there is a term of the form
is a polynomial not contained in this ideal. Without loss of generality we will assume that there is a term of the form  with
with  does not divide
does not divide  . Then
. Then  where
where 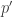 is a non-zero polynomial and so
is a non-zero polynomial and so  is not central.
is not central.
Let us now find all the irreducible finite dimensional representations of  .
.
Taking traces in the identity  , we obtain that any finite dimensional representation
, we obtain that any finite dimensional representation  must be of dimension
must be of dimension 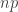 . Suppose
. Suppose  is an eigenvector of
is an eigenvector of  ; say
; say  . We claim that the
. We claim that the  -cyclic space generated by
-cyclic space generated by  is an
is an  -submodule, since it is obviously
-submodule, since it is obviously  -stable and
-stable and

By Schur’s lemma we know that, since  are central and
are central and  is irreducible, their action on
is irreducible, their action on  is scalar. Therefore
is scalar. Therefore  and so
and so  . Moreover, these vectors are linearly independent, since the representation is of dimension
. Moreover, these vectors are linearly independent, since the representation is of dimension 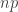 and
and 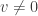 .
.
In conclusion, any finite dimensional representation  must be of dimension
must be of dimension  and there is a basis
and there is a basis  where the action of
where the action of  and
and  is given by matrices
is given by matrices

and conversely different choices of 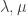 gives rise to non-isomorphic irreducible finite dimensional representations.
gives rise to non-isomorphic irreducible finite dimensional representations.
denote the ring of entire functions (although the following result holds for the ring of holomorphic functions over any complex domain with exactly the same proof). This ring is a domain: if
with
and
entire functions, then the complex plane is the union of the zero locus of
and the zero locus of
. One of these sets must contain an accumulation point (for instance by the Baire category theorem) so it follows that either
or
must be identically zero by the identity principle. This establishes that
is an integral domain.
are precisely the entire functions that vanish nowhere. Moreover, any entire function
with at least two zeroes is reducible: indeed, if
, then
with
entire and vanishing in at least one point, so we have written
as a product of two non-units. It follows that irreducible elements (they exist, although we will not prove it) have exactly one root. Then any non-zero entire function with an infinite amount of zeroes (such as
) cannot be written as a finite product of irreducibles, which proves that
is not a factorial domain.
